Ce week-end, je me suis dit qu’il manquait une corde à mon arc : celle des animations web interactives. J’ai donc décidé de m’y mettre. Je vous raconte comment, et je vous parle des échos sensibles que produisent les fonctions mathématiques dans mon cœur tendre.
Table des matières
Pourquoi utiliser p5.js
Les fana’ de la bidouille numérique ont tous et toutes utilisé une carte Arduino.
Ce mini PC, entièrement programmable, permet d’imaginer et de réaliser à peu près n’importe quel projet numérique. Par exemple, un piano, dont les touches seraient des fruits.
La carte Arduino permet d’enregistrer des signaux d’entrée, comme le fait d’appuyer sur une banane. Puis, on définit des actions à produire en fonction des signaux reçus, comme émettre une note spécifique sur un haut-parleur quand certains fruits sont pressés.
Beaucoup de projets Arduino consistent, plutôt que de produire un son, à produire des visuels. Des visuels qui changent lorsque quelqu’un agit sur un objet connecté à l’Arduino. Des visuels qui réagissent à l’action humaine. Pour ce faire, on utilise généralement un langage qui s’appelle Processing, créé par le MIT Media Lab.
Et bien, un dérivé web de Processing est la librairie Java, p5.js, dédiée à la production d’animations sur le web. Il suffit d’apprendre un peu à parler ce langage, grâce à des tuto disponibles gratuitement sur Internet, pour pouvoir facilement intégrer des objets interactifs sur une page web. Je vous propose de suivre mon chemin.
Les traces en coordonnées polaires.
Pour commencer, je me suis dit qu’il fallait apprendre à créer et manipuler des Objets 3D standard, comme des sphères, puis comprendre comment les altérer. J’ai donc suivi ce tuto :
C’est un jeune japonais qui nous explique, en anglais, le principe des coordonnées polaires, et comment cela peut nous permettre de créer et modifier des formes via des fonctions trigonométriques. Quand je l’écris, ça paraît plus complexe que quand on l’écoute, lui. Si vous avez suivi des études scientifiques, cela devrait vous rappeler des souvenirs.
L’auteur fait son tuto, tard dans la nuit, et chuchote ses explications. Sa voix est douce et reposante. Parfois même, il s’arrête pour contempler la beauté des formes mathématiques et nous offre quelques rappels de fonctions mythiques d’un domaine scientifique qu’on appelle « le traitement du signal ». C’est presque de l’ASMR.
Voyons donc les quelques techniques abordées dans ce tuto.
La sphère « normale »
La sphère dite « normale » est une sphère composée d’anneaux horizontaux, perpendiculaires à l’axe qui joint les deux pôles (voir sur la figure ci-après). Un peu comme les anneaux de latitude de la Terre.

Vous trouverez ici, une page contenant un objet 3D de type sphère « normale » avec lequel vous pouvez jouer. Vous pouvez modifier les paramètres de l’objet : le rayon, ainsi que les angles thêta et phi.
Pour rappel, ces angles sont ceux définis dans un repère polaire. Un repère polaire est un repère où les coordonnées x, y et z, s’expriment en fonction d’une distance et de deux angles.
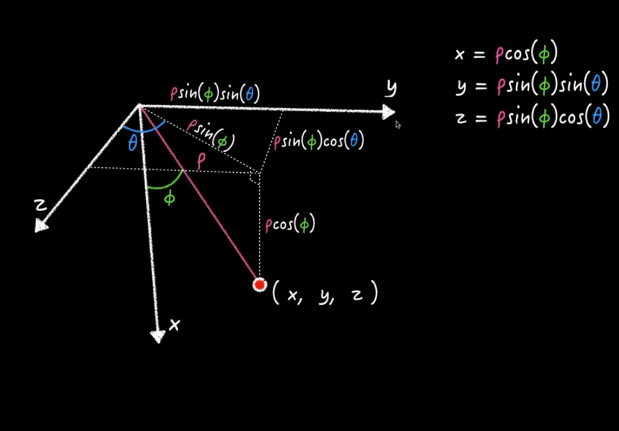
Si l’image manque de clarté, mais que vous comprenez l’anglais, suivez le tuto proposé au début de cette page. C’est très bien expliqué.
Pour voir le code que j’ai utilisé et commenté, c’est ici.
Par rapport au code original, j’ai enlevé la possibilité de contrôler notre vue de l’objet avec la souris. A la place, j’ai imposé une rotation de 0.025 degré sur les axes Y et Z, avec le temps. Cela crée une animation automatique que j’aime bien et qui permet d’admirer l’influence des contraintes qu’on impose sur la forme que prend l’objet.
La sphère « spiralée »
La sphère dite « spiralée » est une sphère dessinée d’un seul fil. Ce fil est comme cloué aux deux pôles, et on peut jouer sur sa longueur, donc sur son entortillement autour de la forme sphérique. Référez-vous à l’image ou au lien ci-après, pour une explication plus visuelle 🙂.

Vous trouverez ici, une page contenant un objet 3D de type sphère « spiralée » avec lequel vous pouvez jouer. Vous pouvez modifier les paramètres de l’objet, à savoir la longueur du fil qui s’enroule autour de la sphère et relie les deux pôles.
Pour voir le code associé à la sphère et aux variateurs, c’est ici. Appréciez comme l’augmentation de la densité donne l’impression d’un fil qu’on enroulerait autour d’une boule. Le tissu du monde.
Lissajous Sphérique
Étant dorénavant capable de représenter une sphère, et de l’animer, en faisant parcourir à des points une ou plusieurs courbes spécifiques à sa surface, on peut s’amuser à représenter des formes plus complexes. Là aussi, ce tuto est intéressant, car il proposera de travailler avec des courbes traditionnelles du traitement du signal, mais en 3D, comme par exemple la courbe de Lissajous.

Vous trouverez ici, une page contenant un objet 3D de type Lissajous pour lequel les fréquences varient automatiquement. Vous noterez que les figures produites varient grandement en fonction du rapport entre ces fréquences.
Pour accéder au code associée à la représentation sphérique de Lissajous, avec des contrôle sur les fréquences, c’est ici.
Remarquez comme, en fonction du rapport que les fréquences entretiennent, l’ensemble parait soit distendu, soit harmonieux.
Les sphères à bosses
Dans la suite du tuto, on apprend a utiliser des « sphères a bosses ». C’est-à-dire des sphères qui peuvent onduler sur leurs axes de latitude et de longitude. C’est comme si une force invisible pouvait faire sortir des montages du sol, en définissant des altitudes et des creux, jusqu’à déchirer la Terre.

Vous trouverez ici, une page ou j’anime une sphère a bosses, que vous pouvez altérer au clavier.
Vous noterez comme une même fonction, avec des arguments qui varient, peut créer des motifs distincts. Cela ferait presque relativiser tout acte de jugement : Chaque point n’est pas soumis aux mêmes remous, selon qu’il se trouve ici ou la, lorsque le programme débute.
Conclusion
Connaissez-vous l’œuvre de 1972, de Pol Bury, intitulée « Sphère molle » ? Vous pourrez la voir dans la boutique du Centre Pompidou, ici.
J’aime bien cette œuvre pour plusieurs raisons. Tout d’abord, visuellement, elle ressemble un peu a la sphère normale du premier chapitre, avec une grande densité, mais qu’on aurait pressée dans une main gigantesque. Ne serait-ce qu’en cela, la sphère molle de Pol Bury se distingue des miennes. Car mes sphères se bossellent plus qu’elles ne s’affaissent. Mais toutes partagent le caractère de « sphère molle ». La sphère molle interroge la pérennité des formes et des images. Peut-on parler de sphère, alors même que cet état ne durera pas plus qu’un autre, au combien différent ? A quelle moment l’étiquette qu’on appose sur l’objet cesse-t-elle d’être suffisante ? Quand le concept devient-il désuet ?
Telles sont les questions auxquelles peut ouvrir ce type d’exercice, qu’il réside dans la contemplation des lignes produites par de savantes équations, ou dans celle faites par les mains d’un·e artiste.
J’espère que vous avez suffisamment exploré ma dernière animation, pour y voir un citron, sinon re-essayez !